Übungen, bei denen Sie Maßeinheiten umrechnen müssen, können Ihnen sowohl in der Schule als auch beim Einstellungstest begegnen.
Wie lange dauert der Test? Wie weit ist es bis zur nächsten Station? Was wiegt der Rucksack? Wie groß ist das Zimmer? Wenn Sie solche Fragen beantworten, nennen Sie nicht nur eine Zahl. Stattdessen geben Sie auch eine Maßeinheit an. Das kann zum Beispiel eine Zeiteinheit, eine Länge oder ein Gewicht sein. Und manchmal müssen Sie die jeweiligen Größen umwandeln, etwa damit Sie unterschiedliche Werte zusammenrechnen können. Doch wie ging das noch mal? Wir erklären anhand von Beispielen und Übungen, wie das Umrechnen von Maßeinheiten funktioniert.
Maßeinheiten umrechnen Übungen im Eignungstest
Mathematik ist ein ständiger Begleiter im Alltag und an vielen Stellen unverzichtbar. Zwar sind es nicht immer komplizierte Rechnungen, die sich mit Zinsen, Prozenten, Vektoren oder geometrischen Fragen befassen. Aber selbst wenn Sie nur Ihren Einkauf an der Supermarktkasse bezahlen, ist Mathe im Spiel.
Aus diesem Grund steht das Rechnen ab der Grundschule bis zur letzten Klasse auf dem Stundenplan. Und auch während der Ausbildung und im Beruf bleibt Ihnen die Mathematik erhalten. Außerdem schreiben Sie nicht nur Klassenarbeiten in Mathe. Sind Sie zu einem Einstellungstest eingeladen, beinhaltet er ebenfalls praktisch immer einen Mathetest. Denn das Rechnen gehört nun mal zu den grundlegenden Fähigkeiten.
Nun reicht es bei vielen Aufgaben aber nicht aus, wenn Sie nur mit Zahlen arbeiten. Stattdessen müssen Sie auch die dazugehörigen Einheiten angeben. Diese wiederum müssen Sie mitunter umwandeln, bevor Sie damit rechnen können.
Und genau dieses Umrechnen von Maßeinheiten zählt zu beliebten Übungen bei Klassenarbeiten und Einstellungstests. Deshalb bringen wir Ihr Wissen zu diesem Thema jetzt auf Vordermann!
Längeneinheiten
Mithilfe von Längeneinheiten beschreiben Sie Längen und Entfernungen. Wenn Sie zum Beispiel angeben möchten, welches Format ein Gegenstand hat, wie weit eine Strecke ist oder welcher Abstand zwischen zwei Punkten liegt, ergänzen Sie die Zahl um eine Einheit wie Zentimeter oder Meter.
Die gängigsten Längeneinheiten und ihre Umwandlung haben wir in der folgenden Tabelle für Sie zusammengefasst:
| Bezeichnung | Einheit | Umrechnung |
|---|---|---|
| Millimeter | mm | 1 mm = 0,1 cm = 0,01 dm = 0,001 m |
| Zentimeter | cm | 10 mm = 1 cm = 0,1 dm = 0,01 m |
| Dezimeter | dm | 100 mm = 10 cm = 1 dm = 0,1 m |
| Meter | m | 1.000 mm = 100 cm = 10 dm = 1 m = 0,001 km |
| Kilometer | km | 1.000.000 mm = 100.000 cm = 1.000 m = 1 km |
Grundsätzlich werden Längen in Metern angegeben. Allerdings macht es nicht immer Sinn, eine Länge oder Entfernung als Meterangabe zu beschreiben. Denn bei sehr kleinen oder sehr großen Entfernungen wäre die Zahl ziemlich umständlich und unübersichtlich. Deshalb wandeln Sie den Wert dann in eine andere Einheit um, die besser passt.
Beim Umrechnen multiplizieren oder dividieren Sie den Wert mit 10, um zur nächst größeren oder kleineren Einheit zu kommen. Das gilt für Millimeter bis Meter. Nur bei der Umwandlung von Meter in Kilometer (oder umgekehrt) rechnen Sie mit dem Faktor 1000:
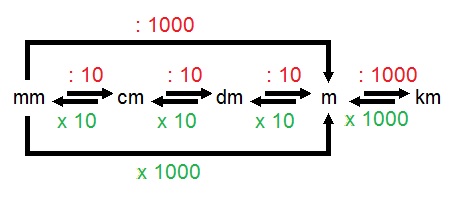
Zum besseren Verständnis ein Beispiel
Angenommen, die Aufgabe lautet, dass Sie 45 Zentimeter auf Meter umrechnen sollen. Dann gibt es zwei Möglichkeiten, wie Sie die Umwandlung durch führen können.
Die erste Möglichkeit ist, dass Sie den Wert zuerst durch 10 teilen, um auf Dezimeter zu kommen. Anschließend dividieren Sie noch einmal durch 10 und erhalten so den Wert in Metern. Sie rechnen also:
0,45 dm : 10 = 0,045 m
Die zweite Möglichkeit ist, dass Sie beide Rechenschritte auf einmal durchführen, indem Sie direkt durch 100 teilen. Denn 10 x 10 = 100.
Flächeneinheiten
Eine Strecke ist eindimensional, denn sie besteht nur aus der Länge. Im Unterschied dazu ist eine Fläche zweidimensional. Sie bestimmt sich nämlich aus der Länge und der Breite. Dabei berechnen Sie eine Fläche, indem Sie die Länge mit der Breite multiplizieren. Das Ergebnis geben Sie anschließend in der jeweiligen Einheit zum Quadrat an.
Wie bei den Längen, wo der Meter die grundlegende Einheit ist, ist bei Flächen der Quadratmeter der Ausgangspunkt. Nun können Flächen aber natürlich die unterschiedlichsten Größen haben. Ein Blatt Papier zum Beispiel ist viel kleiner als ein Zimmer, während ein Land eine viel größere Fläche hat als ein Fußballfeld.
Und damit die Zahl nicht zu groß wird, kommt jeweils die Einheit zum Einsatz, die am besten passt. Dabei stehen folgende Flächeneinheiten zur Auswahl:
| Bezeichnung | Einheit | umgerechnet in Quadratmeter |
|---|---|---|
| Quadratmillimeter | mm2 | 0,000001 m2 |
| Quadratzentimeter | cm2 | 0,0001 m2 |
| Quadratdezimeter | dm2 | 0,01 m2 |
| Quadratmeter | m2 | 1 m2 |
| Ar | a | 100 m2 |
| Hektar | ha | 10.000 m2 |
| Quadratkilometer | km2 | 1.000.000 m2 |
Um Flächeneinheiten umzurechnen, verwenden Sie den Faktor 100. Und weil Sie multiplizieren oder dividieren, kommen Sie auf die Lösung, indem Sie das Komma um zwei Stellen verschieben. Merken Sie sich deshalb:
- Wenn Sie eine kleinere Einheit in die nächst größere Einheit umrechnen, teilen Sie durch 100. Das Komma verschieben Sie dabei um zwei Stellen nach rechts.
- Wollen Sie eine größere Einheit in die nächst kleinere Flächeneinheit umwandeln, multiplizieren Sie mit 100. Das Komma wandert dann um zwei Stellen nach links.
Damit es klarer wird, ein Beispiel
Angenommen, eine Fläche ist 0,85 Hektar groß. Sie sollen die Größe dieser Fläche in Quadratmetern angeben.
Ein Hektar ist größer als ein Quadratmeter. Zwischen diesen beiden Einheiten steht aber noch das Ar. Deshalb müssen Sie entweder erst mit 100 multiplizieren, um auf Ar zu kommen, und anschließend noch einmal mit 100 multiplizieren, um zu den Quadratmetern zu gelangen. Oder Sie rechnen gleich mal 10.000 und verschieben das Komma dafür direkt um vier Stellen nach links.
85 a x 100 = 8.500 m2
0,85 ha x 10.000 = 8.500 m2
Volumeneinheiten
Während Strecken eindimensional und Flächen zweidimensional sind, ist ein Volumen dreidimensional. Es ergibt sich nämlich aus den drei Dimensionen Länge, Breite und Höhe. Dabei beschreibt das Volumen, welchen Inhalt etwas hat.
Um ein Volumen auszurechnen, greifen Sie auf die Längeneinheiten zurück. Die Maße von der Länge, der Breite und der Höhe multiplizieren Sie anschließend miteinander. Das Ergebnis ist dann eine Maßzahl in Kubik. Die gängigsten Volumeneinheiten sind folgende:

- Einstellungstest Komplettkurs für alle Berufe
- Aktuelle Fragen aus diesem Jahr
- Alle Testfelder vorhanden
- Schritt-für-Schritt-Erklärungen aller Lösungen
- Online sofort durchführbar
- über 4500 aktuelle Fragen und Antworten
| Bezeichnung | Einheit | Umwandlung |
|---|---|---|
| Kubikmillimeter | mm3 | 1 mm3 = 0,001 cm3 |
| Kubikzentimeter | cm3 | 1.000 mm3 = 1 cm3 |
| Kubikdezimeter | dm3 | 1.000 cm3 = 1 dm3 |
| Kubikmeter | m3 | 1.000.000 cm3 = 1.000 dm3 = 1 m3 |
Die Umrechnung funktioniert bei den Volumeneinheiten im Prinzip genauso wie bei den Längen- und den Flächeneinheiten. Der Unterschied ist nur, dass Sie beim Volumen mit dem Faktor 1.000 rechnen.
Sie multiplizieren oder dividieren also jeweils mit 1.000, um zur nächst kleineren oder größeren Einheit zu kommen. Das heißt in anderen Worten: Sie fügen drei Nullen dazu oder schneiden drei Nullen ab. Gleichzeitig wandert dadurch auch das Komma jeweils um drei Stellen nach rechts oder links.
Ein Hinweis noch
Manchmal wird ein Volumen nicht in Kubikmetern, sondern in Litern angegeben. Aber auch das ist nicht weiter kompliziert. Sie müssen sich nämlich nur merken:
- Ein Kubikdezimeter entspricht einem Liter.
- Ein Kubikmeter sind 1.000 Liter.
Gewichtseinheiten
Wenn Sie danach gefragt werden, wie viel etwas wiegt, könnten Sie natürlich antworten, dass der Gegenstand ganz leicht oder sehr schwer ist. In der Mathematik und auch in der Physik brauchen Sie aber eine genauere Angabe. Und dafür greifen Sie auf die Gewichtseinheiten zurück.
Der Ausgangspunkt bei der Angabe von Gewichten ist das Gramm. Von hier aus rechnen Sie dann in kleinere oder größere Einheiten um. Die wichtigsten Gewichte haben wir in einer Tabelle für Sie zusammengefasst:
| Bezeichnung | Einheit | Umrechnung |
|---|---|---|
| Milligramm | mg | 1 mg = 0,001 g |
| Gramm | g | 1.000 mg = 1 g = 0,001 kg |
| Kilogramm | kg | 1.000.000 mg = 1.000 g = 1 kg = 0,001 t |
| Tonne | t | 1.000.000.000 mg = 1.000.000 g = 1.000 kg = 1 t |
Wie Sie aus der Tabelle ableiten können, rechnen Sie Gewichtseinheiten mit dem Faktor 1.000 um. Und zwar so:
- Um von einer kleinen Einheit zur nächst größeren zu kommen, teilen Sie durch 1.000.
- Andersherum rechnen Sie eine größere Gewichtseinheit in die nächst kleinere um, indem Sie mit 1.000 multiplizieren.
Oder anders ausgedrückt: Beim Umrechnen verschieben Sie das Komma jeweils um drei Stellen nach rechts oder links.
Ein Beispiel
Laut Aufgabe sollen Sie 750 kg in Tonnen umwandeln. Da die Tonne eine größere Gewichtseinheit ist als das Kilogramm, müssen Sie durch 1.000 teilen. Dazu verschieben Sie das Komma um drei Stellen nach rechts. Das Ergebnis lautet demnach:
Zeiteinheiten
Die Zeiteinheiten kommen ins Spiel, wenn es um die Dauer von etwas geht. Dabei gibt es auch hier verschiedene Einheiten. Die kleinste Zeiteinheit ist die Sekunde, die größte Einheit ist das Jahr. Wie alle anderen Maße können Sie die Dauer ebenfalls in unterschiedlichen Werten angeben und die Einheiten dafür umrechnen.
Zeiteinheiten umzuwandeln, ist allerdings ein bisschen komplizierter. Das liegt daran, dass es keinen einheitlichen Faktor gibt. Stattdessen müssen Sie mit verschiedenen Größen rechnen. Welche Zeiteinheiten es gibt, sehen Sie in der folgenden Tabelle.
| Bezeichnung | Einheit | Umrechnung |
|---|---|---|
| Sekunde | s | 60 s = 1 min |
| Minute | min | 1 min = 60 s |
| Stunde | h | 1 h = 60 min = 3.600 s |
| Tag | d | 1 d = 24 h |
| Woche | Woche | 1 Woche = 7 d |
| Monat | m | 1 m = 28 bis 31 d |
| Jahr | a | 1 a = 12 m = 52 Wochen = 365 oder 366 d |
Bei den Zeiteinheiten bleibt Ihnen letztlich nichts anderes übrig, als sich die Werte einzuprägen. Außerdem müssen Sie ein bisschen aufpassen. Denn nicht immer wird mit den tatsächlichen Größen gerechnet. In der kaufmännischen Zinsrechnung zum Beispiel hat ein Jahr immer nur 360 Tage.
Maßeinheiten umrechnen: Übungen
Nach der ganzen Theorie haben wir jetzt noch ein paar Übungen vorbereitet, mit denen Sie testen können, wie fit Sie im Umrechnen von Maßeinheiten sind.
Wenn Sie in der Schule Arbeitsblätter bearbeiten oder eine Klassenarbeit schreiben, müssen Sie die Maße in aller Regel selbst ausrechnen. Bei einem Einstellungstest ist das ein bisschen anders. Hier werden die Aufgaben nämlich meist als Multiple-Choice-Fragen gestellt.
Multiple Choice bedeutet, dass Sie mehrere Lösungen sehen und daraus die richtige Antwort auswählen müssen. Unsere Übungen zum Umrechnen von Maßeinheiten haben wir ebenfalls als Auswahlfragen gestaltet. Also, los geht’s!
1. Wie viele Kilogramm sind 0,32 Tonnen?
a) 3,2 kg
b) 320 kg
c) 3.200 kg
d) 32.000 kg
2. Wie viele Zentimeter sind 99 Millimeter?
a) 0,0099 cm
b) 0,099 cm
c) 0,99 cm
d) 9,9 cm
3. Welche Umrechnung stimmt?
10,21 m sind …
a) 100.021 mm
b) 1021 cm
c) 10,21 dm
d) 0,1021 km
4. Wie viele Quadratmeter sind 0,41 Hektar?
a) 41 m2
b) 410 m2
c) 4.100 m2
d) 41.000 m2
5. Wie viele Stunden sind eine Woche und zwei Tage?
a) 216 h
b) 238 h
c) 244 h
d) 282 h
6. Wie viele Kubikmeter sind 50 Liter?
a) 5 m3
b) 0,5 m3
c) 0,05 m3
d) 0,005 m3
7. Welche Fläche hat eine Tischplatte, die einen Meter lang und 80 cm breit ist?
a) 0,008 m2
b) 0,08 m2
c) 0,8 m2
d) 8 m2
8. Wie viele Meter sind ein Kubikdezimeter?
a) 10 m
b) 100 m
c) 1.000 m
d) Nichts davon stimmt.
Lösungen
1. b
Eine Tonne entspricht 1.000 Kilogramm. Sie nehmen den Wert deshalb mal 1.000 und kommen damit auf die Lösung 0,32 t x 1.000 = 320 kg
2. d
99 Millimeter sind 9,9 Zentimeter. Denn Sie teilen durch 10, um zur nächst größeren Maßeinheit zu kommen.
3. b
Wenn Sie Längeneinheiten umrechnen, nutzen Sie den Faktor 10, um von einer Einheit zur nächst größeren Einheit zu kommen. 10,21 m sind deshalb 102,1 dm und 1021 cm.
4. c
Ein Hektar entspricht 10.000 Quadratmetern. Folglich ergeben 0,41 Hektar 4.100 Quadratmeter.
5. a
Damit Sie diese Aufgabe ausrechnen können, müssen Sie die Werte zuerst in eine einheitliche Größe bringen.
Eine Woche hat sieben Tage und ein Tag hat 24 Stunden. Folglich hat eine Woche 7 x 24 = 168 Stunden. Dazu kommen noch die Stunden von den beiden zusätzlichen Tagen. 168 Stunden + (2 x 24 Stunden) = 168 Stunden + 48 Stunden = 216 Stunden.
Genauso können Sie natürlich gleich 9 Tage x 24 Stunden rechnen. Auch dann kommen Sie auf 216 Stunden.
6. c
Ein Kubikmeter entspricht 1.000 Litern. Für die Umrechnung müssen Sie deshalb durch 1.000 teilen. Verschieben Sie dazu das Komma um drei Stellen nach rechts, kommen Sie auf 0,05 Kubikmeter als Lösung.
7. c
Um eine Fläche zu berechnen, multiplizieren Sie die Länge mit der Breite. In der Aufgabenstellung sind die Maße aber in unterschiedlichen Einheiten angegeben. Deshalb müssen Sie zunächst umrechnen. Ein Meter entspricht 100 Zentimetern.
Danach können Sie die Größe der Fläche ermitteln: 100 cm x 80 cm = 8.000 cm2.
Da in den Antwortmöglichkeiten aber nur Quadratmeter enthalten sind, müssen Sie Ihren Wert noch durch 1.000 teilen. Durch 1.000 deshalb, weil zwischen den Zentimetern und den Metern noch die Dezimeter stehen. Sie gehen also nicht zur nächsten, sondern zur übernächsten Einheit.
8. d
Der Meter ist eine Längeneinheit, während der Kubikdezimeter eine Volumeneinheit ist. Längen- und Volumenmaße können Sie aber nicht ineinander umwandeln.

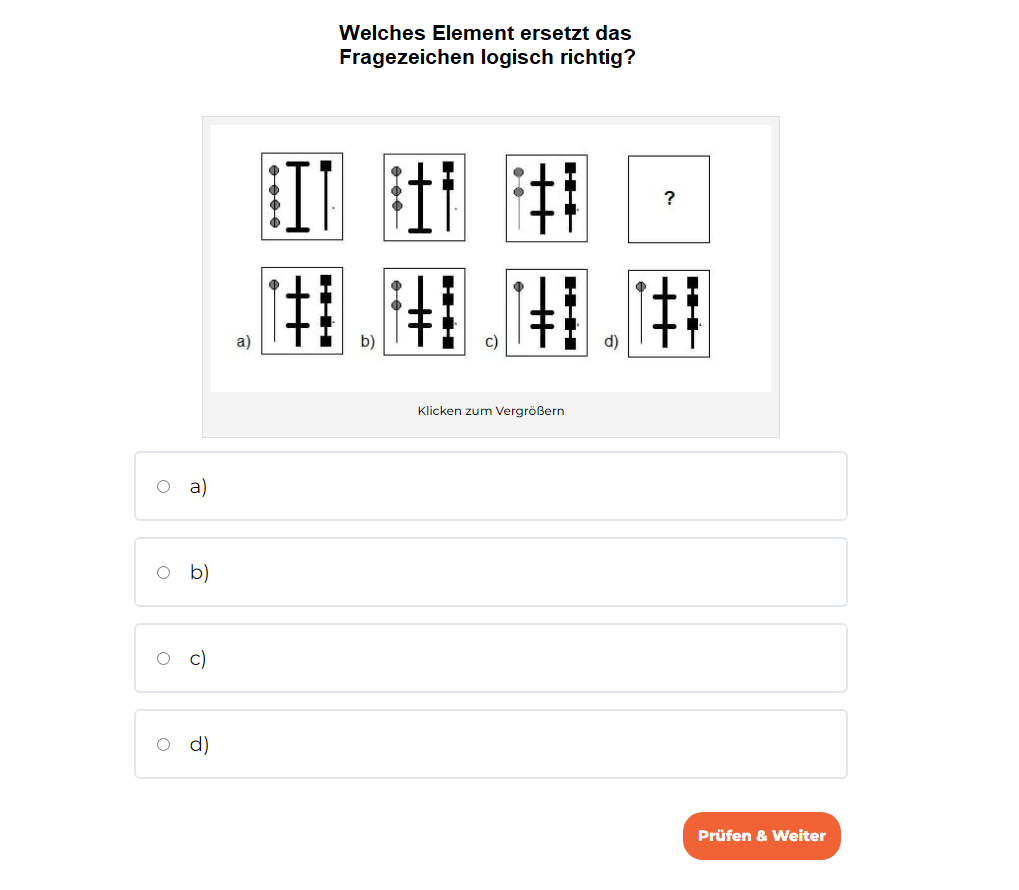 Das Einstellungstest-Übungsmodul bietet eine umfassende Vorbereitung auf Einstellungstests für verschiedene Berufe. Es beinhaltet Übungen zu
Das Einstellungstest-Übungsmodul bietet eine umfassende Vorbereitung auf Einstellungstests für verschiedene Berufe. Es beinhaltet Übungen zu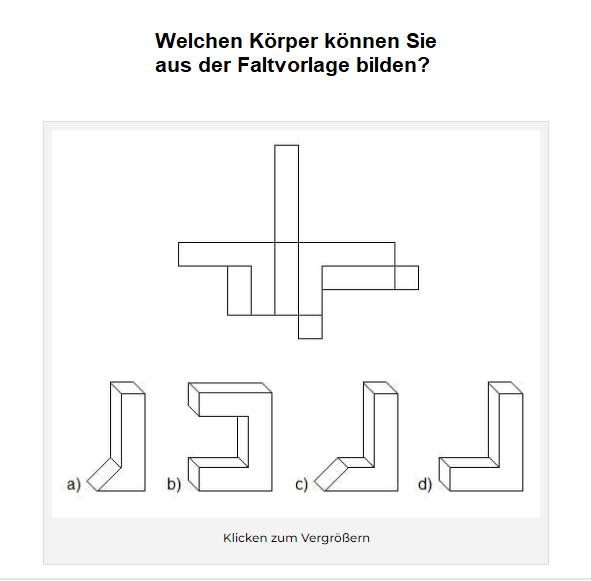
 Deutsch im Einstellungstest
Deutsch im Einstellungstest Allgemeinbildungstest
Allgemeinbildungstest