Wer einmal genau darüber nachdenkt, dass aus Rechtschreibregeln, Zeichensetzungsvorgaben und Fremdwörtern Aufsätze entstehen, der kann dasselbe Phänomen beobachten, wenn aus Subtraktionen, Multiplikationen, Additionen und Divisionen Textaufgaben werden. Mathematische Textaufgaben sind nämlich nichts Weiteres als eine gebündelte Abfrageform für all das Wissen, was im Fachbereich erworben werden kann, deswegen gelten Textaufgaben auch als Königsdisziplin in der Mathematik. Wer Textaufgaben lösen kann, beweist, dass er über ein fundiertes mathematisches Wissen verfügt. Folglich ist der Einstellungstest Mathematisches Denken Textaufgaben auch der Beweis für die Arbeitgeber, dass ein Mitarbeiter Mathe beherrscht. Wie gut Sie in Mathematik sind, können Sie nun bei diesen Übungsaufgaben unter Beweis stellen. Hinweis: Wir haben in diesem Beitrag auf die bloße Angabe der Antwort verzichtet und versucht, möglichst detailliert die Lösungswege zu skizzieren. Wir hoffen, Ihnen damit eine langfristige Hilfestellung bei der Beantwortung ähnlicher Fragen geben zu können.
Wer einmal genau darüber nachdenkt, dass aus Rechtschreibregeln, Zeichensetzungsvorgaben und Fremdwörtern Aufsätze entstehen, der kann dasselbe Phänomen beobachten, wenn aus Subtraktionen, Multiplikationen, Additionen und Divisionen Textaufgaben werden. Mathematische Textaufgaben sind nämlich nichts Weiteres als eine gebündelte Abfrageform für all das Wissen, was im Fachbereich erworben werden kann, deswegen gelten Textaufgaben auch als Königsdisziplin in der Mathematik. Wer Textaufgaben lösen kann, beweist, dass er über ein fundiertes mathematisches Wissen verfügt. Folglich ist der Einstellungstest Mathematisches Denken Textaufgaben auch der Beweis für die Arbeitgeber, dass ein Mitarbeiter Mathe beherrscht. Wie gut Sie in Mathematik sind, können Sie nun bei diesen Übungsaufgaben unter Beweis stellen. Hinweis: Wir haben in diesem Beitrag auf die bloße Angabe der Antwort verzichtet und versucht, möglichst detailliert die Lösungswege zu skizzieren. Wir hoffen, Ihnen damit eine langfristige Hilfestellung bei der Beantwortung ähnlicher Fragen geben zu können.
Einstellungstest Mathematisches Denken Textaufgaben
Aufgabe 1: Die Freunde Niklas und Mia wohnen 58 Kilometer auseinander. Damit keiner der beiden zu weit zu fahren hat, wollen sie sich in der Mitte treffen. Mia startet um 13:30 Uhr. Niklas beginnt seine Radtour um 13:50 Uhr. Niklas fährt mit 21 Stundenkilometern, Mia mit 18. Wo treffen sich die Freunde?
Lösungsweg: Zunächst muss in mathematischen Worten (also in Zahlen und Buchstaben) notiert werden, was eigentlich bekannt ist und auch, was gesucht ist. Das hilft, einen Überblick zu schaffen über die bevorstehende Aufgabe. Diese Informationen liegen vor:
- Mia fährt 18 Stundenkilometer schnell (v = 18). Mia trifft dort auf Niklas, wo er zu radeln aufhört (x = 58 – y). Mia fährt mit 18 km/h und braucht daher für die Strecke (t = x / 18).
- Niklas fährt 21 Stundenkilometer schnell (v = 21). Niklas trifft auf Mia, wo sie zu radeln aufhört (y = 58 – x). Niklas fährt mit 21 km/h und startet 20 Minuten später (= 1/3 Stunde) (t = y / 21 + 1/3).
Unabhängig davon, wann sie gestartet sind, treffen sich die Freunde jedoch zur gleichen Zeit, also ist t Niklas = t Mia. Das heißt auch: x / 18 = y / 21 + 1 / 3. Diese Gleichung gilt es nun aufzulösen. Zunächst wird diese Gleichung mit 18 multipliziert. Dann ergibt sich diese Gleichung: x= 18 / 21 y + 18 / 3 = 18 / 21 y + 6. Diese Gleichung wird nun in die Fahrtstreckengleichung von Niklas eingesetzt:
y = 58 – 18 / 21 y + 6 oder gekürzt: y = 52 – 18 / 21 y
Mit nur einer Variablen in der Gleichung kann diese entsprechend umgestellt und aufgelöst werden.
y = 52 – 18 / 21 y | Zu dieser Gleichung wird 18 / 21 y addiert.
39 / 21 y = 52 | Diese Gleichung wird durch 39 / 21 dividiert.
y = 1092 / 39 = 28

- Einstellungstest Komplettkurs für alle Berufe
- Aktuelle Fragen aus diesem Jahr
- Alle Testfelder vorhanden
- Schritt-für-Schritt-Erklärungen aller Lösungen
- Online sofort durchführbar
- über 4500 aktuelle Fragen und Antworten
Da y die Variable für Niklas‘ Wegstrecke war, ist nun klar, dass er 28 Kilometer gefahren ist, bis er auf seine Freundin Mia getroffen ist. Da eine Gesamtstrecke von 58 Kilometern zwischen den Freunden lag, muss Mia folgerichtig 30 Kilometer gefahren sein, um am selben Ort und zur selben Zeit auf Niklas zu treffen.
Aufgabe 2: Patrick ist vier Jahre älter als seine Schwester Mathea. In zehn Jahren wird Patrick doppelt so alt sein wie seine Schwester Mathea heute ist. Wie alt ist das Geschwisterpaar heute?
Lösungsweg: Zunächst einmal werden die geschriebenen Worte in mathematische Worte umfunktioniert. So wird aus dem Alter von Patrick ein „P“ und aus dem Alter von Mathea wird ein „M“. Zudem gilt, dass Patrick heute vier Jahre älter ist als Mathea. In einer mathematischen Formel bedeutet das: P = M + 4. Da Patrick in zehn Jahren doppelt so alt sein wird wie seine Schwester Mathea heute ist, gilt: P + 10 = 2 M. Nun wird die erste Gleichung in die zweite eingesetzt, um nur noch eine Variable zu erhalten.
M + 4 + 10 = 2M
Zieht man nun von beiden Seiten ein M ab, erhält man diese finale Gleichung:
4 + 10 = 14 = M
Wenn klar ist, dass Mathea 14 Jahre alt ist, dann ist Patrick vier Jahre älter und damit 18 Jahre. So lautet die Lösung: Mathea ist 14 Jahre alt und Patrick ist 18.
Aufgabe 3: Sabrina und Vanessa sind Cousinen. Heute sind sie zusammengerechnet 28 Jahre alt. Nächstes Jahr ist Sabrina doppelt so alt wie ihre Cousine Vanessa. Doch wie alt sind die beiden Mädchen heute?
Lösungsweg: Auch an dieser Stelle gilt (wie in der Regel üblich bei Textaufgaben), dass zunächst die Worte in Mathematik übersetzt werden müssen. S ist dabei das Alter von Sabrina, V das Alter von Vanessa. Die gegebenen Werte können zu diesen beiden Formeln umgebaut werden:
- Gemeinsam sind die Mädchen 28 Jahre: S + V = 28
- In einem Jahr ist Sabrina zweimal so alt wie Vanessa: (S + 1) = 2 (V + 1)
Um nun dem Ergebnis ein Stückchen näher kommen zu können, muss versucht werden, die eine Variable mit der anderen zu ersetzen. Umgestellt heißt die erste Gleichung (a) dann S = 28 – V. Dieser Term wird nun in die zweite Gleichung (b) eingesetzt [(S + 1) = 28 – V + 1]. Das Ergebnis dieses Zwischenschrittes lautet: 28 – V + 1 = 2 (V + 1).
Nun geht es darum, diese Gleichung nach der Variable V aufzulösen, um im ersten Schritt herauszubekommen, wie alt Vanessa heute ist. In den folgenden Zwischenschritten kommen Sie dann zum Ergebnis:
29 – V = 2V + 2 | Von dieser Gleichung wird 2 subtrahiert und V addiert.
27 = 3V | Diese Gleichung wird durch den Faktor 3 dividiert.
Als Ergebnis steht nun fest V = 9. Da V als Variable für Vanessas Alter steht, ist Vanessa neun Jahre alt. Sabrina ist 28 minus 9 Jahre alt und damit 19 Jahre alt.
Der Einstellungstest Mathematisches Denken Textaufgaben
Textaufgaben müssen kein Buch mit sieben Siegeln sein, sie sind lediglich die komprimierte Abfrage mehrerer mathematischer Methoden. Grundsätzlich gilt bei Textaufgaben immer dieser Ablaufplan:
- Übersetzen Sie die Angaben aus Worten in Zahlen und Gleichungen.
- Setzen Sie Gleichungen in andere Gleichungen ein, um die Anzahl der Variablen zu minimieren.
- Lösen Sie die Gleichungen nach den Variablen auf.
- Notieren Sie eine Antwort, die wiederum ein ganzer Satz und damit auch aussagekräftig ist.

 Das Einstellungstest-Übungsmodul bietet eine umfassende Vorbereitung auf Einstellungstests für verschiedene Berufe. Es beinhaltet Übungen zu
Das Einstellungstest-Übungsmodul bietet eine umfassende Vorbereitung auf Einstellungstests für verschiedene Berufe. Es beinhaltet Übungen zu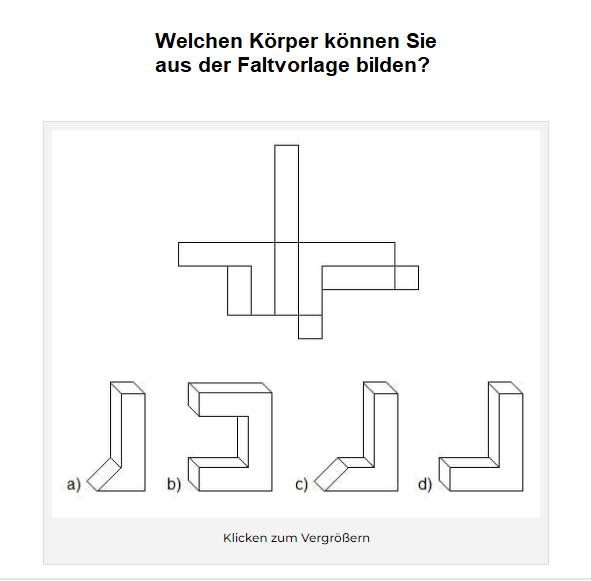
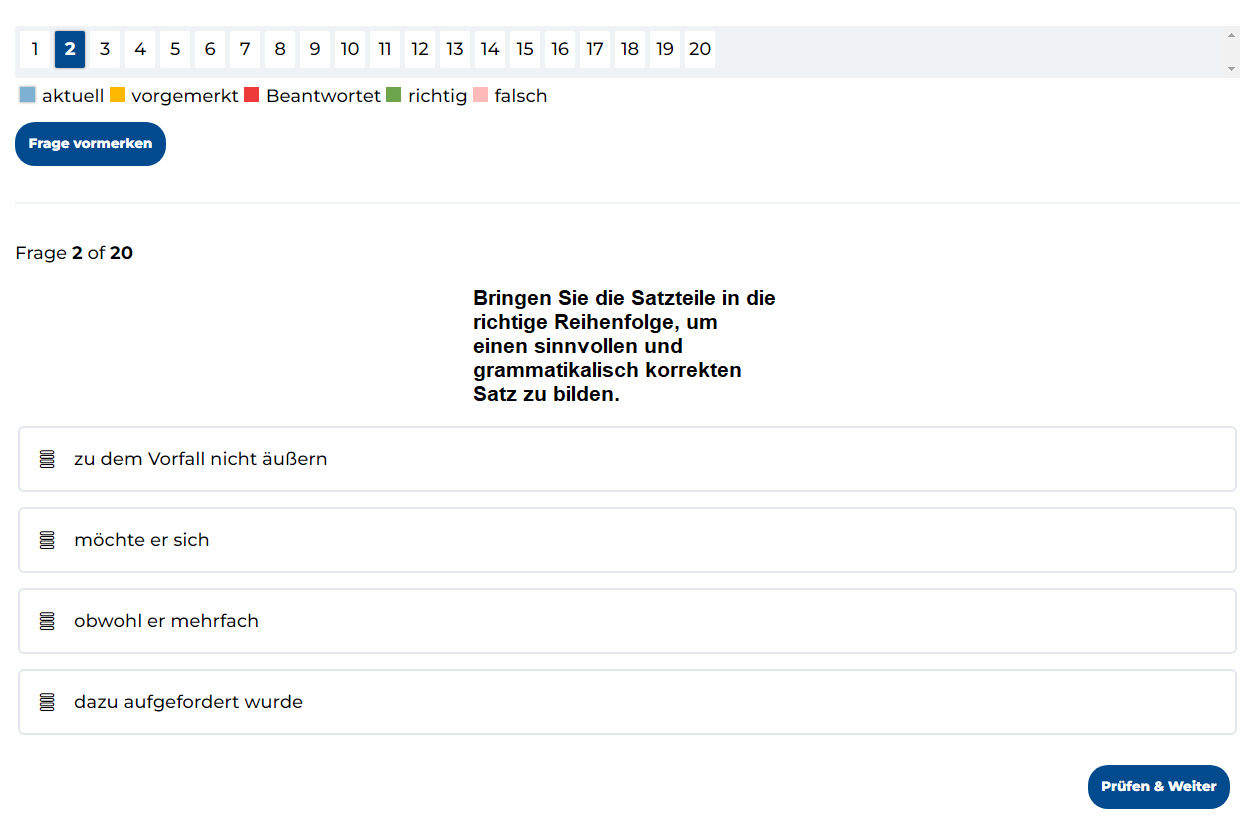 Deutsch im Einstellungstest
Deutsch im Einstellungstest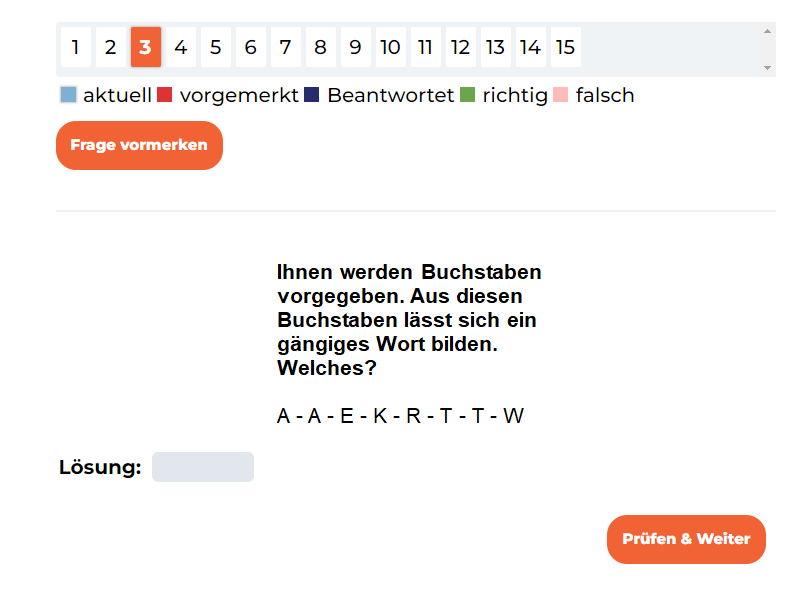 Allgemeinbildungstest
Allgemeinbildungstest