Der wohl am meisten gefürchtete Test ist der Einstellungstest Logisches Denken Zahlenreihen. Unser Ziel ist es nun, dass Sie diese Meinung nach diesem Beitrag revidieren, denn wir möchten Ihnen Herangehensweisen erklären, um die Logik hinter Zahlenreihen zu erschließen – und den Test lösen zu können. Diejenigen, die sich nun fragen, wofür diese Form von logischem Denkvermögen benötigt wird, denen sei gesagt: Auch im Berufsleben werden Ihnen Aufgaben gestellt, die einem bestimmten Muster folgen. Wenn Sie lernen, wie Sie diese Muster erkennen können, erlernen Sie auch, wie Sie sie erneut anwenden können und darauf baut letztlich jede effiziente und strukturierte Arbeitsweise auf: Auf der Grundidee, Muster zu erkennen und diese wieder anwenden zu können. Sie brauchen Ihr logisches Denkvermögen also nicht etwa nur einmalig für den Einstellungstest Logisches Denken Zahlenreihen – sondern auch für Ihr Berufsleben. Wir erklären Ihnen, welche Logik hinter Zahlenreihen stecken kann.
Einstellungstest Logisches Denken Zahlenreihen
Ganz grundsätzlich sehen Zahlenreihen auf den ersten Blick immer erstmal verwirrend aus und so mancher fragt sich: Welches Muster soll dahinter stecken? Versuchen Sie als Erstes die Gruppen ausfindig zu machen, die Sie bilden können. Das heißt, dass es verschiedene Gruppen gibt, die zueinander korrelieren. In der nächsten Tabelle sehen Sie einige Beispiele:
| Keine Gruppe | 5 – 15 – 25 – 35 – 45 – 55 – … | Bei dieser Zahlenreihe wird auf den ersten Blick deutlich, dass es eine ganz klassische Entwicklung der Zahlen ist. Von Zahl zu Zahl wird um zehn Punkte weitergesprungen. |
| Zweiergruppe | 3 – 75 – 13 – 70 – 23 – 65 – 33 – 60 – … | Eine Zweiergruppe bedeutet, dass jede zweite Zahl zusammenhängt. Das heißt, dass von 3 zu 13 zu 23 zu 33 immer die Zahl 10 addiert wurde. Das ist die Zahlengruppe 1 in unserem Beispiel. In der Zahlengruppe 2 wird von 75 zu 70 zu 65 zu 60 immer die Zahl 5 subtrahiert. |
| Dreiergruppe | 21 – 8 – 36 – 14 – 16 – 40 – 7 – 24 – 44 – … | Eine Dreiergruppe bedeutet, dass jede dritte Zahl zusammenhängt. Zahlengruppe 1 springt von 21 zu 14 zu 7, subtrahiert also immer die Zahl 7. Zahlengruppe 2 springt von 8 zu 16 zu 24 und addiert also immer die Zahl 8. Zahlengruppe 3 springt von 36 zu 40 zu 44 und addiert also immer die Zahl 4. |
Haben Sie die Gruppen ausfindig gemacht, gibt es verschiedene Beziehungen, die zwischen den Zahlen möglich sein können. Addition und Subtraktion, die bereits angedeutet wurden, sind dabei nur zwei Rechenvarianten, die beim Einstellungstest logisches Denken Zahlenreihen möglich wären. Lern-Tipp: Wer sich nun an das kleine Einmaleins erinnert fühlt, der hat absolut Recht, denn wer dieses beherrscht, der wird manchmal leichter erkennen können, welche Gruppen zusammengehören und welche Zahlen addiert oder subtrahiert werden.
Fall 1: Summen und Differenzen
Die simpelste und dabei auch häufigste Form im Einstellungstest logisches Denken Zahlenreihen ist die Bildung von Summen und Differenzen. Das heißt, dass die Zahlen in ihren Zahlengruppen entweder addiert oder subtrahiert werden, oder anders: Die Zahlen werden gedanklich dazugezählt oder eben abgezogen. Nach zwei Beispielen inklusive Erklärung haben wir einige Übungsaufgaben für Sie gelistet:
Beispiel 1: 7 – 72 – 14 – 64 – 21 – 56 – 28 – 48 – X – Y.
- Einstellungstest Komplettkurs für alle Berufe
- Aktuelle Fragen aus diesem Jahr
- Alle Testfelder vorhanden
- Schritt-für-Schritt-Erklärungen aller Lösungen
- Online sofort durchführbar
- über 4500 aktuelle Fragen und Antworten
Ergebnis und Erklärung: Hierbei handelt es sich um eine Zweiergruppe. Gruppe 1 (7-14-21-28-X) addiert immer die Zahl 7 auf. Gruppe 2 (72-64-56-48-Y) zieht immer die Zahl 8 ab. So lautet das Ergebnis für X= 35 und Y= 40.
Beispiel 2: 13 – 96 – 35 – 18 – 90 – 42 – 23 – 84 – 49 – X – Y – Z.
Ergebnis und Erklärung: Hierbei handelt es sich um eine Dreiergruppe. Gruppe 1 (13-18-23-X) addiert immer die Zahl 5 auf. Gruppe 2 (96-90-84-Y) zieht immer die Zahl 6 ab. Gruppe 3 (35-42-49-Z) addiert immer die Zahl 7 auf. So lautet das Ergebnis so: X= 28, Y= 78, Z= 56.
Übungsaufgaben:
- 37 – 2 – 38 – 4 – 39 – 6 – 49 – 8 – 50 – 10 – 51 – 12 – X – Y. (Lösung: X= 61, Y= 14)
- 88 – 6 – 77 – 12 – 66 – 18 – 55 – 12 – 44 – 6 – X – Y. (Lösung: X= 33, Y= 12)
- 17 – 6 – 37 – 26 – 57 – 46 – 77 – 66 – X – Y. (Lösung: X= 97, Y= 86)
Fall 2: Multiplikationen und Divisionen
Etwas schwieriger wird es, wenn nicht nur Zahlen zusammengerechnet oder voneinander abgezogen werden, sondern auch wenn mit Multiplikationen und Divisionen gearbeitet wird, sprich wenn Zahlen miteinander multipliziert (malgenommen) oder dividiert (geteilt) werden. Hier zeigt sich einmal mehr, wer gute Kenntnisse der Einmaleins-Rechnungen hat, denn diese Kenntnisse helfen an dieser Stelle enorm viel weiter. Nach zwei Beispielen inklusive Lösung und Erklärung folgen auch hier Übungsaufgaben.
Beispiel 1: 2 – 7 – 4 – 49 – 16 – 2401 – X – Y.
Ergebnis und Erklärung: Hierbei handelt es sich um eine Zweiergruppe. Gruppe 1 (2-4-16-X) multipliziert sich immer mit sich selbst. 2 mal 2 macht 4, 4 mal 4 macht 16, 16 mal 16 macht X= 256. Gruppe 2 (7-49-2401-Y) multipliziert sich immer ebenfalls immer mit sich selbst. 7 mal 7 macht 49, 49 mal 49 macht 2401, 2401 mal 2401 macht Y= 5.764.801.
Beispiel 2: 250 – 3 – 50 – 6 – 10 – 12 – X – Y.
Ergebnis und Erklärung: Hierbei handelt es sich um eine Zweiergruppe. Gruppe 1 (250-50-10-X) wird durch die Zahl 5 dividiert. Folglich ist X=2. Bei Gruppe 2 (3-6-12-Y) wird das jeweilige Ergebnis immer mit 2 multipliziert. Das heißt, dass Y= 24 ist.
Übungsaufgaben:
- 6 – 72 – 36 – 9 – 9 – 18 – 54 – 3 – X – Y. (Lösung: X= 54, Y= 3)
- 21 – 4 – 3 – 20 -15 – 140 – X – Y. (Lösung: X= 30, Y=1260)
- 35 – 36 – 7 – 4 – 49 – 32 – 7 – 8 – X –Y. (Lösung: X= 35, Y= 36)
Achtung: Mathematische Sonderfälle
Neben den Mathematik-Klassikern können unter Umständen auch mathematische Sonderregeln in den Zahlenreihen versteckt sein. Aufmerksam sollten Sie werden, wenn Sie die Zahlen 2, 3, 5, 7, 11, 13, 17 und 19 sehen. Diese hängen zwar nicht durch ein Rechenzeichen bedingt zusammen, gehören aber zu einer ganz bestimmten Gruppe an Zahlen, nämlich zu den Primzahlen, die nur durch sich selbst und die Zahl 1 teilbar sind. Eine Übersicht aller Primzahlen können Sie hier abrufen. Grundsätzlich ist es sinnvoll, die Vorbereitung auf den Einstellungstest Logisches Denken Zahlenreihen mit der Vorbereitung auf den Mathematiktest zu koppeln, den wie Sie bereits selbst gesehen haben, sind diverse Parallelen zu verzeichnen. Zudem waren die Zahlenreihen nur ein Teil des Einstellungstestes logisches Denken, den diesen gibt es auch für Domino-Serien, Grafik-Analogien oder Figurenreihen.
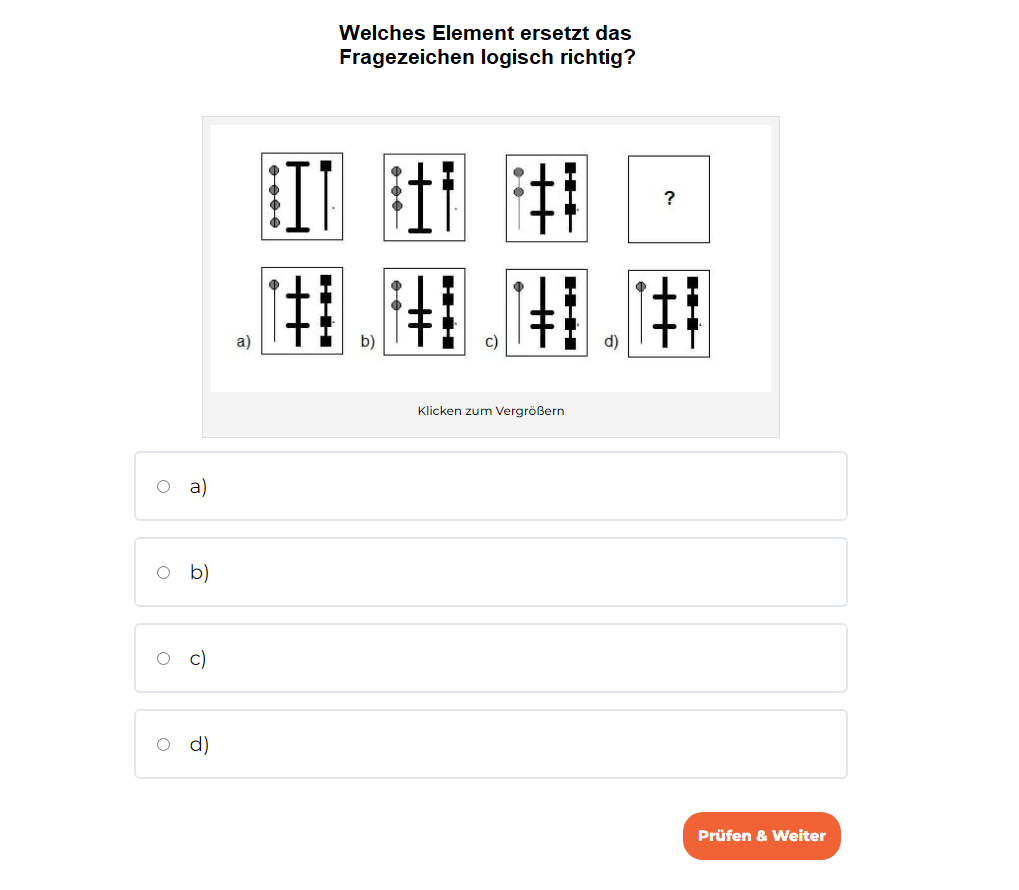Das Einstellungstest-Übungsmodul bietet eine umfassende Vorbereitung auf Einstellungstests für verschiedene Berufe. Es beinhaltet Übungen zu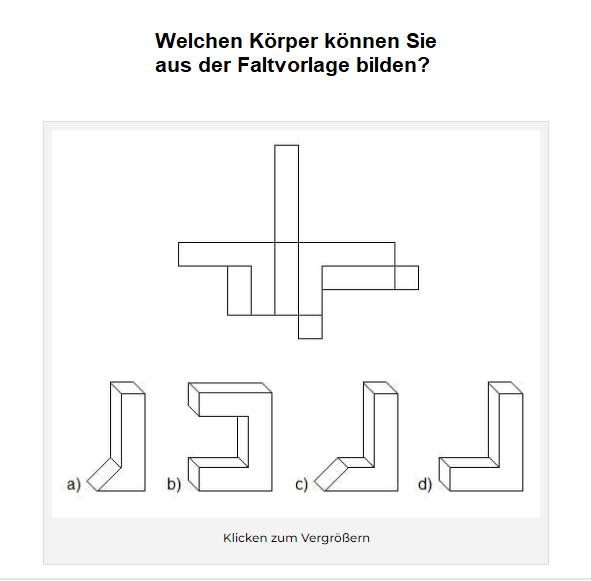
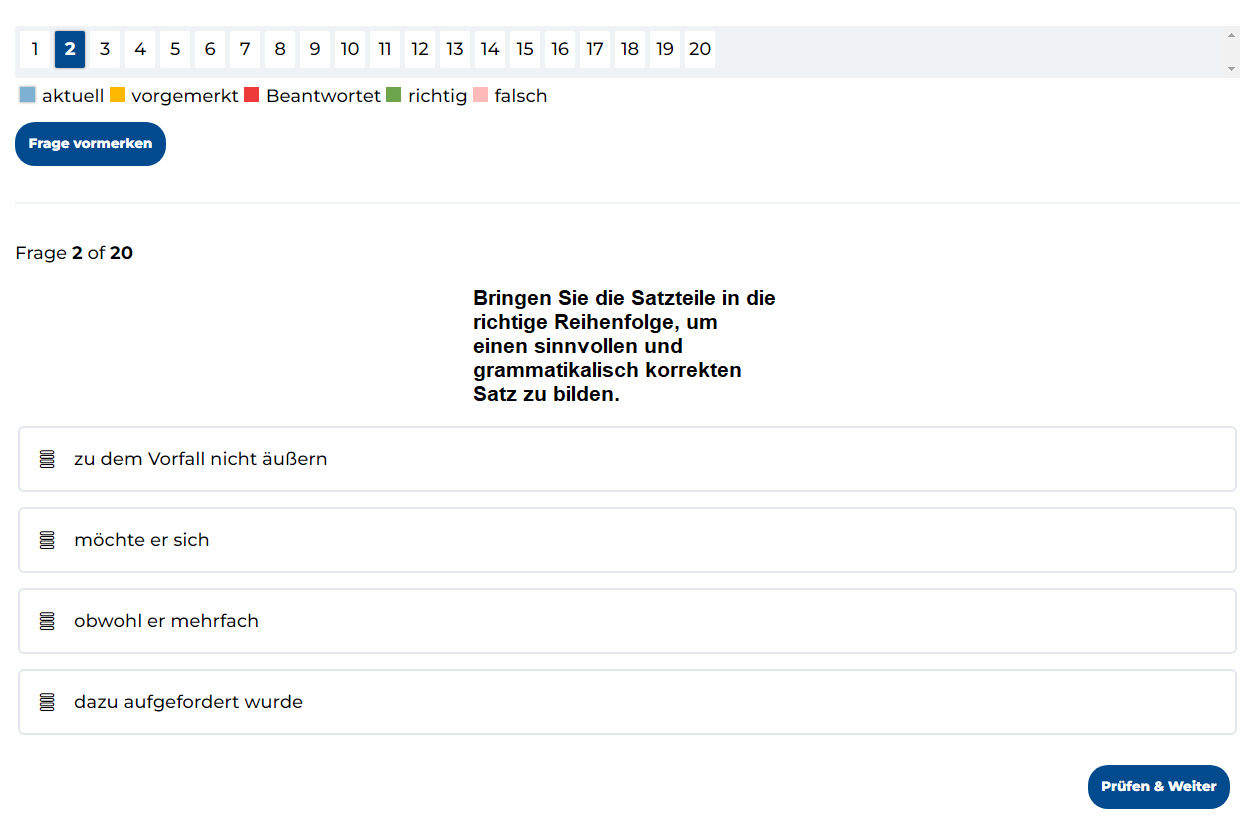Deutsch im Einstellungstest
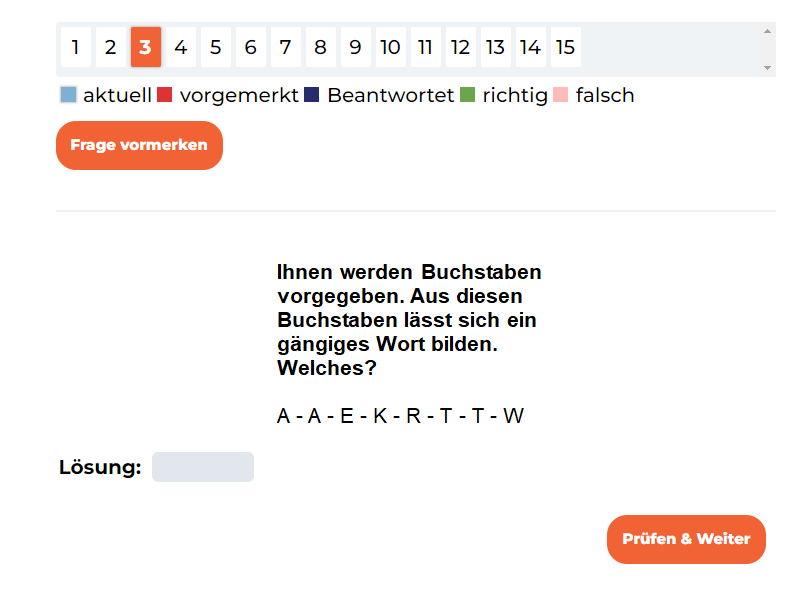Allgemeinbildungstest
