„Du darfst doch nicht Äpfel mit Birnen vergleichen!“ Wer diese mahnenden Worte in erster Linie vom Mathematik- oder Physik-Lehrer gehört hat, der hat meist ein- und denselben, eklatanten Fehler gemacht: Er hat sich weder um Maße noch Gewichte gekümmert und bei der Berechnung buchstäblich alles in einen Topf geworfen. Das Resultat dabei war dann, dass das Ergebnis der Berechnung falsch oder ohne Inhalt war, denn ohne die Angabe von Maß und Gewicht hat eine Zahl nur selten einen Aussagewert. Sie fragen sich, ob diese Fehler oft gemacht werden? Ja, sie zählen mit zu den häufigsten Fehlern (neben Fehlern in Prozent- und Zinsrechnung). Da Sie im Mathematiktest vor allem aber auch bei den Ihnen gestellten Textaufgaben auf ganzer Linie versagen werden, haben wir dieses Kapitel den Maßen und Gewichten gewidmet. Hier können Sie nachschlagen und üben, um sich auf den Einstellungstest Mathematisches Denken Maße und Gewichte vorzubereiten.
Einstellungstest Mathematisches Denken Maße und Gewichte
Umrechnen leicht gemacht – mit diesen Nachschlagetabellen
Um eine Basis zu schaffen, um überhaupt die Übungen für den Einstellungstest Mathematische Denken Maße und Gewichte absolvieren zu können, haben wir Ihnen zunächst Übersichtstabellen kreiert, die die wichtigsten Maßeinheiten aufgreifen. Hier können Sie Ihr Wissen testen und Wissenslücken gegebenenfalls schließen.
| Umrechnungstabelle Länge | ||||
| 1 mm | = 0,1 cm | = 0,01 dm | = 0,001 m | = 0,000 001 km |
| 10 mm | = 1 cm | = 0,1 dm | = 0,01 m | = 0,000 01 km |
| 100 mm | = 10 cm | = 1 dm | = 0,1 m | = 0,000 1 km |
| 1.000 mm | = 100 cm | = 10 dm | = 1 m | = 0,001 km |
| 1.000.000 mm | = 100.000 cm | = 10.000 dm | = 1.000 m | = 1 km |
| Umrechnungstabelle Fläche | ||||
| 1 mm² | = 0,01 cm² | = 0,000 1 dm² | = 0,000 001 m² | = 0,000 000 000 001 km² |
| 100 mm² | = 1 cm² | = 0,1 dm² | = 0,000 1 m² | = 0,000 000 000 1 km² |
| 10.000 mm² | = 100 cm² | = 1 dm² | = 0,01 m² | = 0,000 000 01 km² |
| 1.000.000 mm² | = 10.000 cm² | = 100 dm² | = 1 m² | = 0,000 001 km² |
| 1.000.000.000.000 m² | = 10.000.000.000 cm² | = 100.000.000 dm² | = 1.000.000 m² | = 1 km² |
| Umrechnungstabelle Volumen | ||||
| 1 mm³ | = 0,001 cm³ | = 0,000 001 dm³ | = 0,000 000 01 m³ | = 0,000 000 000 000 000 001 km³ |
| 1.000 mm³ | = 1 cm³ | = 0,001 dm³ | = 0,000 001 m³ | = 0,000 000 000 000 001 km³ |
| 1.000.000 mm³ | = 1.000 cm³ | = 1 dm³ | = 0,001 m³ | = 0,000 000 000 001 km³ |
| 1.000.000.000 m³ | = 1.000.000 cm³ | = 1.000 dm³ | = 1 m³ | = 0,000 000 001 km³ |
1.000.000.000.
000.000.000 mmm³ |
= 1.000.000.000.
000.000 cm³ |
= 1.000.000.000.
000 dm³ |
= 1.000.000.000 m³ | = 1 km³ |
| Umrechnungstabelle Gewicht | |||
| 1 mg | = 0,001 g | = 0,000 001 kg | = 0,000 000 001 t |
| 1.000 mg | = 1 g | = 0,001 kg | = 0,000 001 t |
| 1.000.000 mg | = 1.000 g | = 1 kg | = 0,001 t |
| 1.000.000.000 mg | = 1.000.000 g | = 1.000 kg | = 1 t |
| Umrechnungstabelle Zeit | |||
| 1 s | = 0,166666666666 min | = 0,00027777777778 h | = 0,00001157407407 d |
| 60 s | = 1 min | = 0,0166666666666 h | = 0,00069444444445 d |
| 3.600 s | = 60 min | = 1 h | = 0,04166666666664 d |
| 86.400 s | = 1.440 min | = 24 h | = 1 d |
Lerntipp: Einstellungstest Mathematisches Denken Maße und Gewichte
Einen ersten Lernerfolg können Sie bereits erzielen, wenn Sie die soeben genannten Umrechnungstabellen beherrschen. Um diese üben zu können, können Sie sich eine entsprechende Blanko-Tabelle anfertigen, um diese dann – ohne zu spicken – auszufüllen.
Übungsaufgaben zum Einstellungstest Mathematisches Denken Maße und Gewichte
Aufgabe 1: Füllen Sie die Lücken der folgenden Gleichungen.
- 6 m² = _______ dm² = _______ cm² (Lösung: 6 m² = 600 dm² = 60.000 cm²)
- _______ m² = _______ dm² = 125.000 cm² (Lösung: 12,5 m² = 1.250 dm² = 125.00m cm²)
- _______ cm² = 1.500 dm² = _______ m² (Lösung: 150.000 cm² = 1.500 dm² = 15 m²)
- 000 cm² = _______ dm² = _______ m² (Lösung: 30.000 cm² = 300 dm² = 3 m²)
- 1,02 m² = _______ dm² = _______ cm² (Lösung: 1,02 m² = 102 dm² = 10.200 cm²)
- 20,77 m = _____ m _____ cm = _____ m _____ dm _____ cm (Lösung: 20,77 m = 20 m 77 cm = 20 m 2 dm 7 cm)
- 28,9 dm = _____ dm _____ cm = _____ m _____ dm _____ cm (Lösung: 28,9 dm = 28 dm 9 cm = 2 m 8 dm 9 cm)
- 78,4 cm = _____ cm _____ mm (Lösung: 78,4 cm = 78 cm 4 mm)
- 24,7 km = _____ km _____ m = _____ m (Lösung: 24,7 km = 24 km 700 m = 24.700 m)
- 0,008 km = _____ m (Lösung: 0,008 km = 8 m)
Aufgabe 2: Ein Spielfeld, das neu auf der Freifläche des Kindergartens angelegt werden soll, hat die Form eines Rechtecks. Es ist 25 Meter lang und 12 Meter breit.
2.1. Wie groß ist das Spielfeld?
Lösung: Um die Spielflächen-Größe herauszufinden, müssen die Längen multipliziert werden. 35 x 12 = 420 m². So misst die Spielfläche, die entstehen soll, 420 m².
2.2. Rund um die Spielfläche soll ein Weg entstehen, den die Kinder zum Roller- oder Bobbycar-Fahren nutzen können. Welchen Flächeninhalt wird dieser Weg haben, wenn er 1,8 Meter breit angelegt wird?
Lösung: Zunächst wird die Fläche berechnet, die der Weg entlang der Längsseiten einnimmt [1,8 + 35 +1,8 =38,6 m]. Diese Summe wird mit der Wegbreite multipliziert [38,6 x 1,8 = 69,48 m²]. Da der Weg an beiden Längsseiten verläuft, muss diese Zahl mal 2 multipliziert werden [69,48 m² x 2 = 138,96 m²]. Für die Breitseiten gilt folgende Berechnung: 12 x 1,8 = 21,6 m² x 2 = 43,2 m². Summa Summarum wird der Weg dann eine Fläche von 138,96 m² + 43,2 m² = 182,16 m² haben.
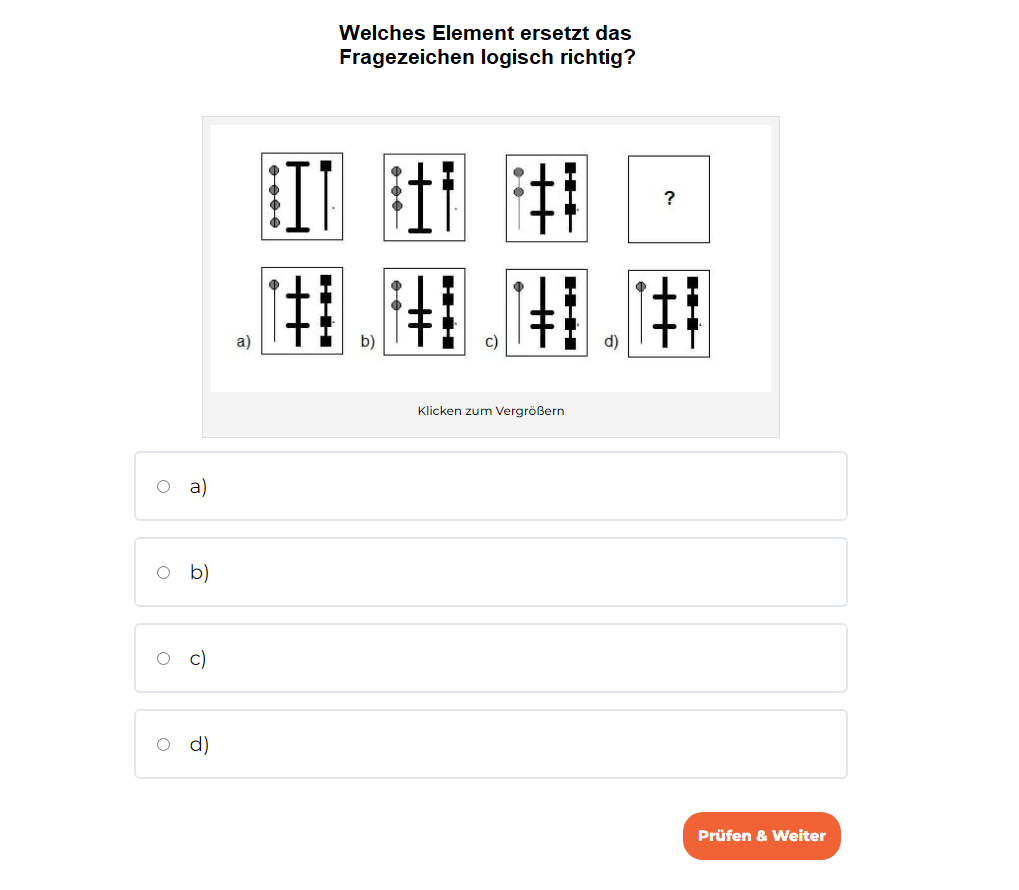Das Einstellungstest-Übungsmodul bietet eine umfassende Vorbereitung auf Einstellungstests für verschiedene Berufe. Es beinhaltet Übungen zu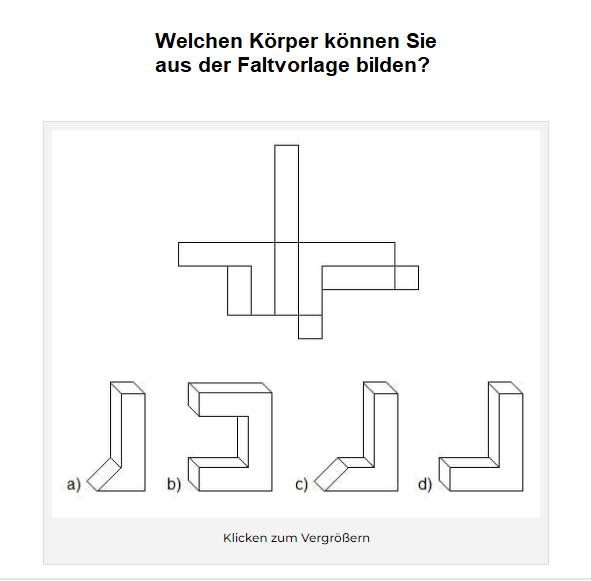
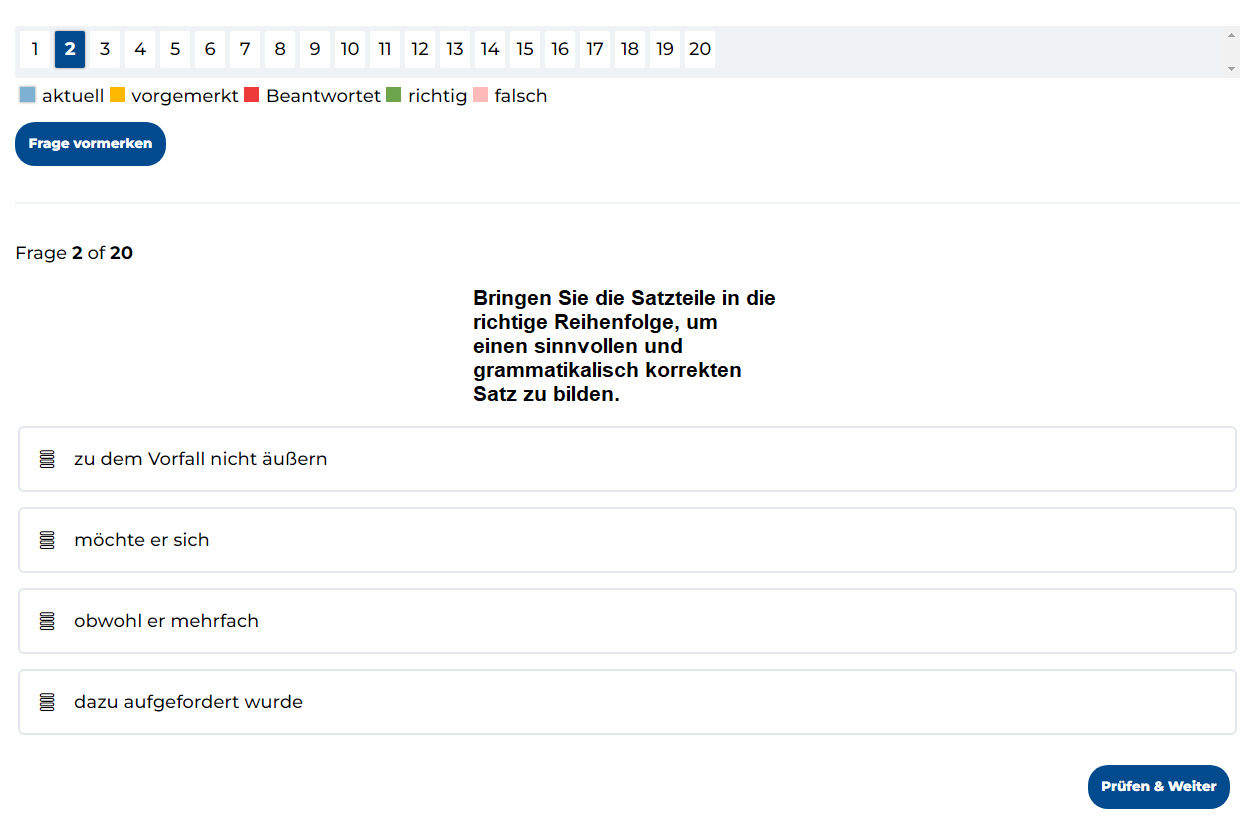Deutsch im Einstellungstest
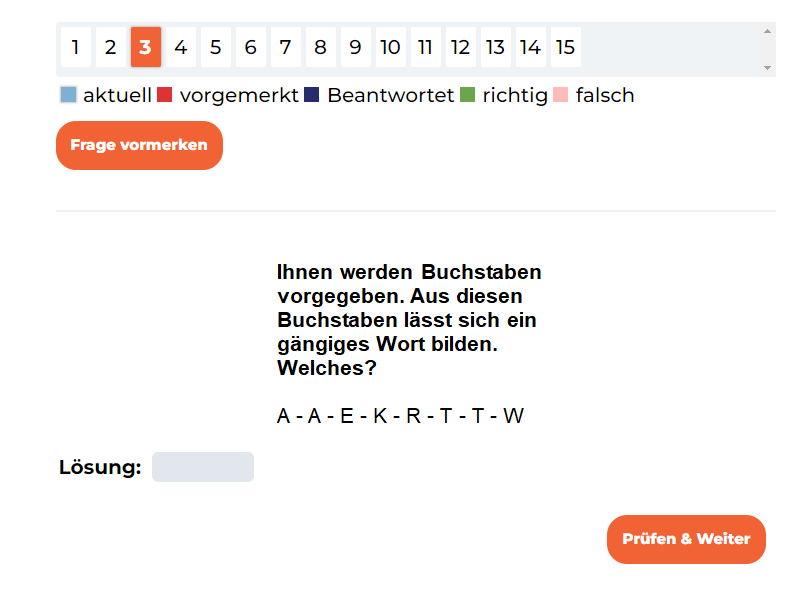Allgemeinbildungstest
