„Deutsche Mädchen hassen Mathe.“ So lautet eine Überschrift, die in Zusammenhang mit der PISA-Studie im Deutschlandfunk einen Artikel einleitet, der sagt, dass Mädchen grundsätzlich schlechter in Mathematik sind als Jungs. Statistisch betrachtet liegen die Mädchen in diesem Fach 14 Punkte hinter den gleichaltrigen Jungs. Allerdings gelte diese Tendenz nur in Deutschland, heißt es weiter. Zudem brachte die PISA-Studie noch ein weiteres spannendes Details an Tageslicht und das heißt: Selbst wenn Mädchen besser in Mathe abschneiden als Jungs, stehen sie dem Fach doch mit einer negativen Grundhaltung gegenüber. Sie haben in Mathe weniger Ausdauer und auch weniger Motivation, sich mit dem Jonglieren von Zahlen zu beschäftigen. Die Ergebnisse aus der PISA-Studie werden mit denen aus der OECD untermauert. Dort heißt es, dass die mathematischen Fähigkeiten einen entscheidenden Einfluss auf den späteren Beruf haben? Ob darin der Grund begraben liegt, dass der Einstellungstest Mathe vielen ein Dort im Auge ist bzw. viele buchstäblich Angst davor haben? Mag sein. Nötig ist das nicht, denn wer sich gezielt vorbereitet, kann den Einstellungstest Mathe bestehen.
Einstellungstest Mathe
Einstellungstest Mathe: Aufgaben, die ohne Taschenrechner zu lösen sind
Für viele ist allein schon diese Einleitung Neuland. Auch wenn in den meisten Einstellungstests Mathe ein Taschenrechner erlaubt ist und zur Grundausstattung gehört, muss das nicht immer zwingend der Fall sein. Für die folgenden Bruchrechnungen nutzen Sie bitte Ihren Kopf – und nicht den Taschenrechner.
- 1/3 + 5/12 = … (Lösung: 3/4)
- 6/18 + 2/6 = … (Lösung: 2/3)
- 4/4 – 8/2 = … (Lösung: -3)
- 7/8 – 1/4 = … (Lösung: 5/8)
- 6/9 x 2/8 = … (Lösung: 1/6)
- 5/6 x 3/5 = … (Lösung: 1/2)
- 7/2 : 5/6 = … (Lösung: 21/5)
- 9/2 : 1/2 = … (Lösung: 9)
Nachholbedarf beim Bruchrechnen? So geht’s!
Falls Sie jetzt gemerkt haben, dass Ihnen die Aufgaben nicht so leicht von der Hand gegangen sind, wie angenommen, nennen wir Ihnen gerne nochmal die drei Grundregeln, die beim Rechnen mit Brüchen zu beachten sind:
- Die Addition/Subtraktion von Brüchen funktioniert so: Die Brüche müssen zunächst auf einen Nenner gebracht werden, dann können die Zähler addiert/subtrahiert werden. Der Ergebnisbruch wird dann gekürzt.
- Die Multiplikation von Brüchen funktioniert so: Die Zähler werden multipliziert, die Nenner werden multipliziert. Der Ergebnisbruch wird dann gekürzt.
- Die Division von Brüchen funktioniert so: Um Brüche zu dividieren, werden sie mit dem Kehrwert multipliziert. Der Ergebnisbruch wird dann gekürzt.
Einstellungstest Mathe: Die größte Fehlerquelle sind Prozentrechnungen
Jetzt mal Hand aufs Herz. Stehen überdimensional große Prozentzeichen auf einem Sale-Schild, ist das das Positivste, was einem Shopping-Fan nur passieren kann. Nur wenn es um das Berechnen von Prozenten geht, dann überfällt viele der Horror. Testen Sie Ihre Kenntnisse mit den folgenden Aufgaben:
- Einstellungstest Komplettkurs für alle Berufe
- Aktuelle Fragen aus diesem Jahr
- Alle Testfelder vorhanden
- Schritt-für-Schritt-Erklärungen aller Lösungen
- Online sofort durchführbar
- über 4500 aktuelle Fragen und Antworten
- Ein Handtuchset kostet 19,90 Euro. Der Einkaufspreis lag bei 14,50 Euro. Beantworten Sie nun die folgenden Fragen:
- Um wie viel Prozent ist der Einkaufspreis zum Verkaufspreis gestiegen? (Lösung: Der Verkaufspreis ist um 37,2 Prozent angestiegen.)
- Wie hoch (gemessen in Prozent) ist der Einkaufspreis? (Lösung: Der Einkaufspreis liegt bei 72,9 Prozent in Bezug auf den Verkaufspreis.)
- Am Rabattsamstag gibt es 25 Prozent Nachlass. Was kostet das Handtuchset dann? (Lösung: Am Rabattsamstag kostet das Handtuchset 14,92 Euro.)
- Ein Controller nimmt die Personalkosten der letzten Jahre unter die Lupe. Im Jahr 2012 wurden 320.500 Euro an Gehältern ausgezahlt. Im Folgejahr wurden 333.500 Euro an Gehältern ausgezahlt. Von welchem prozentualen Anstieg spricht der Controller hier in diesem Beispiel? (Lösung: Der prozentuale Anstieg liegt bei 4,1 Prozent.)
- Ein Planungsbüro hat den Auftrag einen Festplatz im Ort zu errichten. Dieser soll 70 Meter lang und 50 Meter breit sein.
- Wie würde sich die Fläche verändern, wenn der Platz um zehn Prozent verlängert würde? (Lösung: Der Flächeninhalt würde um zehn Prozent steigen.)
- Was würde passieren, wenn anstatt der Länge, die Breite um zehn Prozent gesteigert würde? (Lösung: Der Flächeninhalt würde um zehn Prozent steigen.)
Nachholbedarf beim Prozentrechnen? So geht’s!
Auch für das vermeintlich schwierige Prozentrechnungen gibt es vier grundlegende Hinweise, die zum Ergebnis führen. G steht in den folgenden Formeln für Grundwert, p% für Prozentsatz, p für Prozentzahl und W für Prozentwert.
- W = p x G / 100
- P% = W / G
- P = 100 x W / G
- G = 100 x W / p
Einstellungstest Mathe: Eins, zwei Dreisatz!?
Als das zweite Schreckgespenst neben der Prozentrechnung hat sich mittlerweile der Dreisatz herausgestellt. Ob Sie sich auch vor diesen Aufgaben fürchten müssen, erfahren Sie nach der Lösung der folgenden Aufgaben:
- Drei Solarleuchten für den Garten kosten zusammen 12 Euro. Was steht auf der Rechnung, wenn acht Lampen gekauft werden? (Lösung: Acht Lampen kosten 32 Euro.)
- Laut Tankstellenradar soll es an einer bestimmten Tankstelle im Ort sehr günstigen Sprit geben. 80 Liter kosten dort 120 Euro. Hannes’ Tank ist jedoch nicht ganz leer. Was muss er für 20 Liter Benzin bezahlen? (Lösung: Hannes muss für eine Tankfüllung mit 20 Litern 30 Euro bezahlen.)
- Familie Kraus macht einen Großeinkauf auf dem Markt. Ein Sack mit 50 Äpfeln kostet 25,20 Euro steht auf dem Schild eines Händlers geschrieben. Da 50 Äpfel doch etwas zu viel für die vierköpfige Familie sind, muss Kerstin nun ausrechnen, was 20 Äpfel kosten würden, um die Kosten mit anderen vergleichen zu können. (Lösung: Kerstins Ergebnis lautet: 20 Äpfel kosten 10,08 Euro.)
Nachholbedarf beim Dreisatz? So geht’s!
Ganz grundsätzlich wird ein Dreisatz in dieser Reihenfolge berechnet: (1) Ausgangssituation notieren, (2) eine Rechenart wählen, die eine Seite auf 0 setzt, (3) eine Rechenart wählen, die das gesuchte Ergebnis erreicht. Dabei spielt immer auch die Proportionalität eine Rolle.
- Ist ein Zusammenhang proportional, bedeutet das, dass beide Seiten steigen. Beispiel: Je mehr ich einkaufe, desto mehr muss ich dafür bezahlen.
- Ist ein Zusammenhang antiproportional, bedeutet das, dass eine Seite steigt und die andere Seite sinkt. Beispiel: Je mehr Personen zu einer Tippgemeinschaft gehören, desto geringer wird der Einzelgewinn für jeden ausfallen.
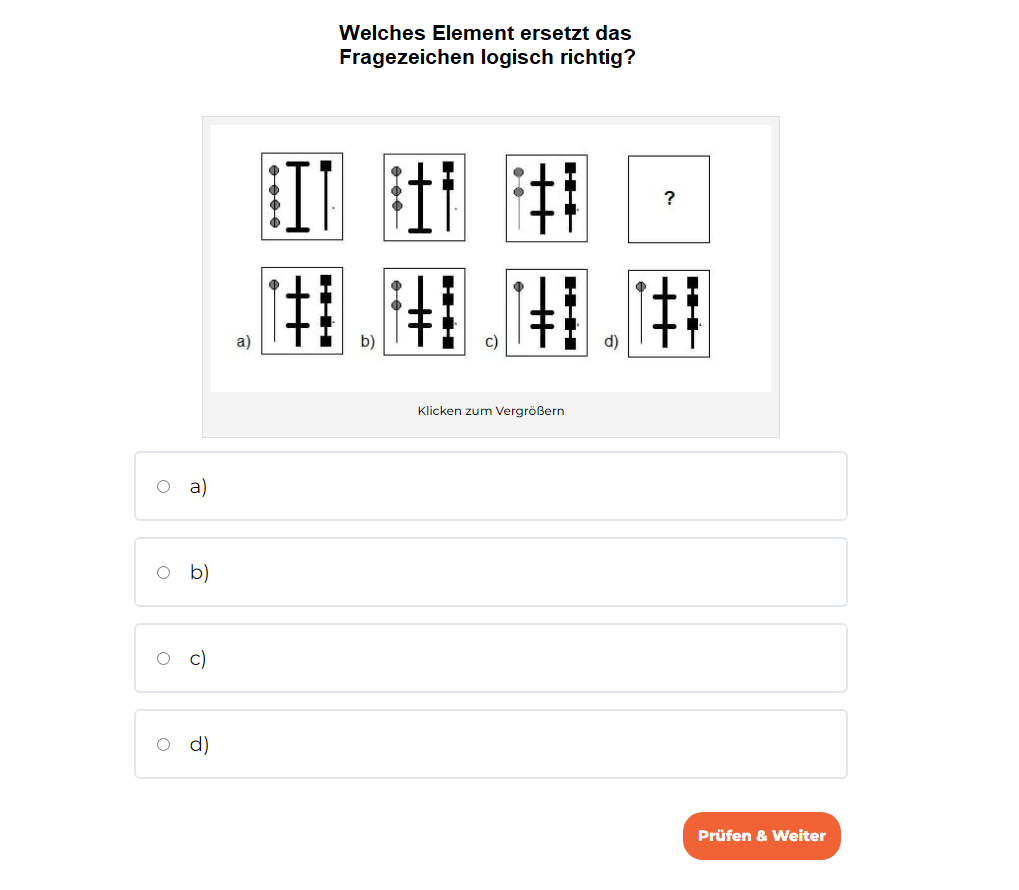Das Einstellungstest-Übungsmodul bietet eine umfassende Vorbereitung auf Einstellungstests für verschiedene Berufe. Es beinhaltet Übungen zu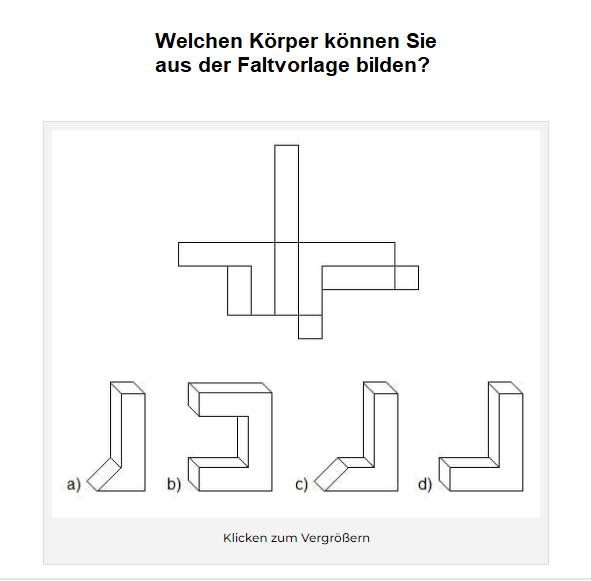
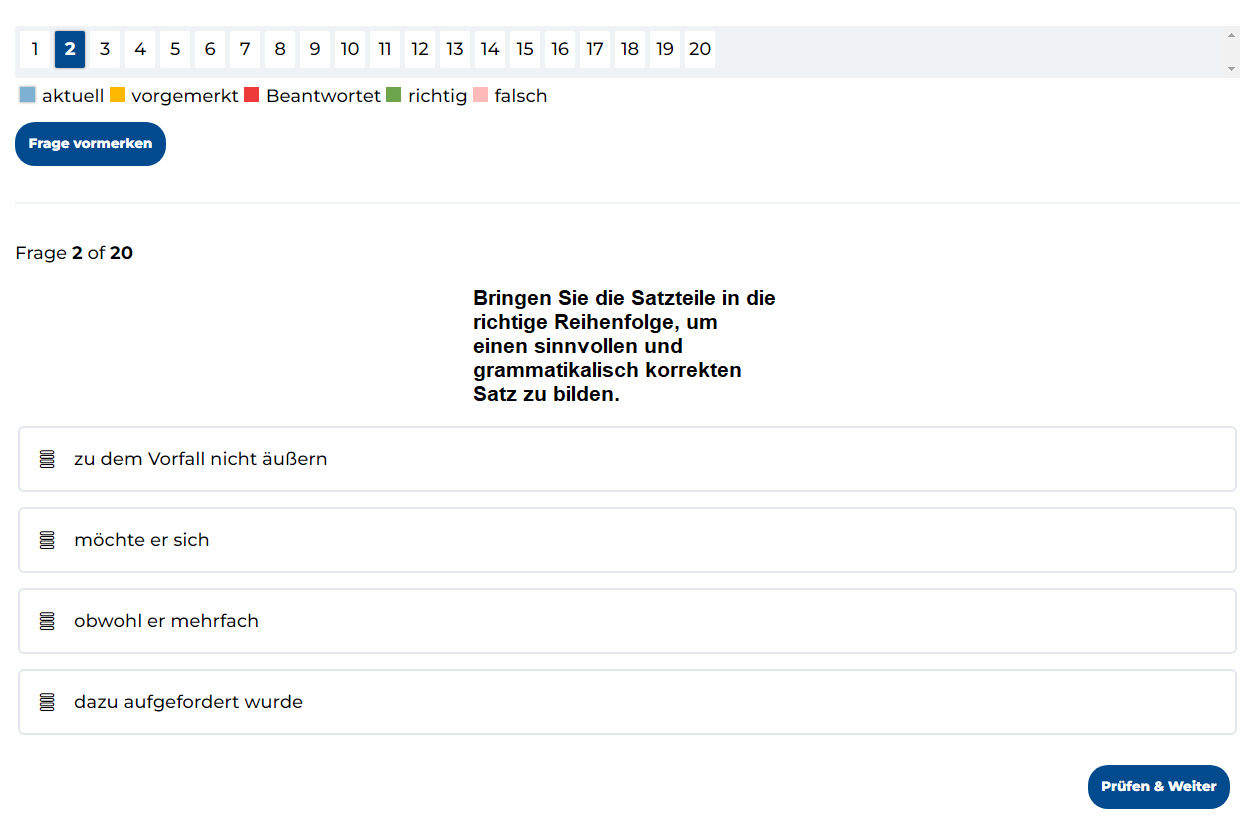Deutsch im Einstellungstest
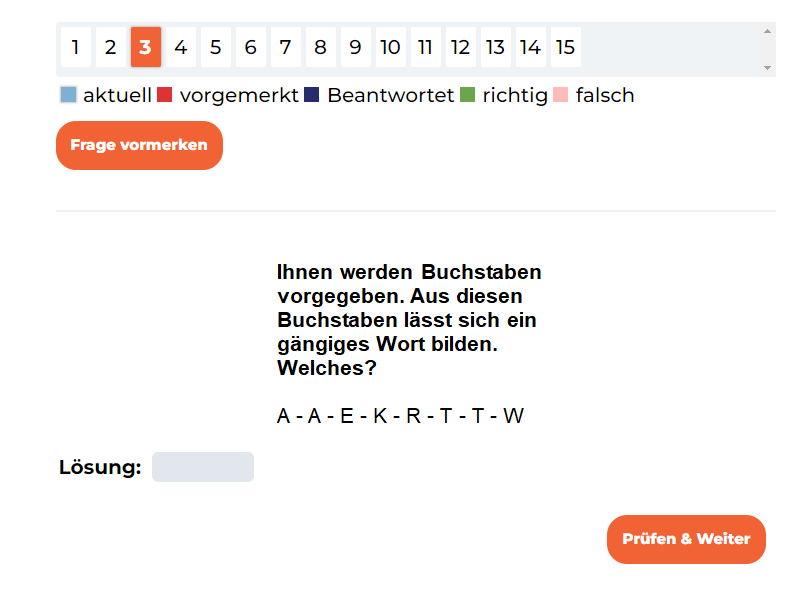Allgemeinbildungstest
